पाठ – 5
यूक्लिड की ज्यामिति का परिचय
In this post we have given the detailed notes of class 9 Math chapter 5 Introduction to Euclid’s Geometry in Hindi. These notes are useful for the students who are going to appear in class 9 board exams.
इस पोस्ट में कक्षा 9 के गणित के पाठ 5 यूक्लिड की ज्यामिति का परिचय के नोट्स दिये गए है। यह उन सभी विद्यार्थियों के लिए आवश्यक है जो इस वर्ष कक्षा 9 में है एवं गणित विषय पढ़ रहे है।
| Board | CBSE Board, UP Board, JAC Board, Bihar Board, HBSE Board, UBSE Board, PSEB Board, RBSE Board, CGBSE Board, MPBSE Board |
| Textbook | NCERT |
| Class | Class 9 |
| Subject | Math |
| Chapter no. | Chapter 5 |
| Chapter Name | यूक्लिड की ज्यामिति का परिचय (Introduction to Euclid’s Geometry) |
| Category | Class 9 Math Notes in Hindi |
| Medium | Hindi |
पाठ 5, यूक्लिड की ज्यामिति का परिचय
यूक्लिड की ज्यामिति
- शब्द ज्यामिति (Geometry) ग्रीक शब्द “जियो”(Geo) से आया है, जिसका अर्थ है “पृथ्वी”, और “मेट्रॉन”,(Metron) जिसका अर्थ है “मापना”। यूक्लिडियन ज्यामिति एक गणितीय प्रणाली है जिसका श्रेय मिस्र में अलेक्जेंड्रिया में गणित के शिक्षक यूक्लिड को दिया जाता है। यूक्लिड ने हमें अपनी पुस्तक “एलिमेंट्स” में ज्यामिति की बुनियादी अवधारणाओं के बारे में एक असाधारण विचार दिया।
- यूक्लिड ने महसूस किया कि ज्यामिति का सटीक विकास नींव से शुरू होना चाहिए।
- ज्यामिति की बेहतर समझ के लिए यूक्लिड के अभिगृहीतों और अभिधारणाओं का अभी भी अध्ययन किया जाता है।
- यूक्लिडियन ज्यामिति ज्यामितीय आकृतियों (तल और ठोस) और विभिन्न स्वयंसिद्धों और प्रमेयों पर आधारित आकृतियों का अध्ययन है। यह मूल रूप से समतल सतहों के लिए पेश किया गया है।यूक्लिडियन ज्यामिति को विशेष रूप से ज्यामितीय आकृतियों और विमानों के आकार के लिए बेहतर ढंग से समझाया गया है। ज्यामिति के इस भाग का प्रयोग यूनानी गणितज्ञ यूक्लिड ने किया था, जिन्होंने इसका वर्णन अपनी पुस्तक एलिमेंट्स में भी किया है। इसलिए, इस ज्यामिति को यूक्लिड ज्यामिति भी कहा जाता है।अभिगृहीत या अभिधारणाएँ ऐसी मान्यताएँ हैं जो स्पष्ट सार्वभौमिक सत्य हैं, वे सिद्ध नहीं होती हैं। यूक्लिड ने अपनी पुस्तक के तत्वों में ज्यामिति के मूल सिद्धांतों जैसे ज्यामितीय आकृतियों और आकृतियों का परिचय दिया है और 5 मुख्य स्वयंसिद्ध या अभिधारणाएँ बताई हैं। यहां, हम यूक्लिडियन ज्यामिति की परिभाषा, इसके तत्वों, अभिगृहीतों और पांच महत्वपूर्ण अभिधारणाओं पर चर्चा करने जा रहे हैं।
यूक्लिड की परिभाषाएँ, अभिगृहीत और अभिधारणाएँ
यूक्लिड ने इन कथनों को संक्षिप्त रूप से परिभाषाओं के रूप में प्रस्तुत किया। उन्होंने अपने इन रहस्योदघाटनों का प्रारम्भ ‘एलीमेंट्स’ की पुस्तक 1 में 23 परिभाषाएँ देकर किया। इनमें से कुछ परिभाषाएँ नीचे दी जा रही हैंः
परिभाषाएँ
- एक बिंदु वह है जिसका कोई भाग नहीं होता।
- एक रेखा चौड़ाई रहित लम्बाई होती है।
- एक रेखा के सिरे बिंदु होते हैं।
- एक सीधी रेखा ऐसी रेखा है जो स्वयं पर बिंदुओं के साथ सपाट रूप से स्थित होती है।
- एक पृष्ठ वह है जिसकी केवल लम्बाई और चौड़ाई होती है।
- पृष्ठ के किनारे रेखाएँ होती हैं।
- एक समतल पृष्ठ ऐसा पृष्ठ है जो स्वयं पर सीधी रेखाओं के साथ सपाट रूप से स्थित होता है।
अभिगृहीत
- यूक्लिड के कुछ अभिगृहीतों को, बिना उनके द्वारा दिए क्रम के, नीचे दिया जा रहा हैः
- वे वस्तुएँ जो एक ही वस्तु के बराबर हों एक दूसरे के बराबर होती हैं।
- यदि बराबरों को बराबरों में जोड़ा जाए, तो पूर्ण भी बराबर होते हैं।
- यदि बराबरों को बराबरों में से घटाया जाए, तो शेषफल भी बराबर होते हैं।
- वे वस्तुएँ जो परस्पर संपाती हों, एक दूसरे के बराबर होती हैं।
- पूर्ण अपने भाग से बड़ा होता है।
- एक ही वस्तुओं के दुगुने परस्पर बराबर होते हैं।
- एक ही वस्तुओं के आधे परस्पर बराबर होते हैं।
प्रमेय 5.1: दो भिन्न रेखाओं में एक से अधिक बिंदु उभयनिष्ठ नहीं हो सकता।
उपपत्ति
- यहाँ, हमें दो रेखाएँ l और m दी हुई हैं। हमें यह सिद्ध करना है कि l और m में केवल एक बिंदु उभयनिष्ठ है।
- थोड़े समय के लिए, यह मान लीजिए कि ये दो रेखाएँ दो भिन्न बिंदुओं P और Q पर प्रतिच्छेद करती हैं।
- इस प्रकार, दो भिन्न बिंदुओं P और Q से होकर जाने वाली आपके पास दो रेखाएँ l और m हो जाती हैं। परन्तु यह कथन अभिगृहीत 5-1 के विरुद्ध है, जिसके अनुसार दो भिन्न बिंदुओं से होकर एक अद्वितीय रेखा खींची जा सकती है। अतः, हम जिस कल्पना से चले थे कि दो रेखाएँ दो भिन्न बिंदुओं से होकर जाती हैं गलत है।
- इससे यह निष्कर्ष निकलता है कि दो भिन्न रेखाओं में एक से अधिक बिंदु उभयनिष्ठ नहीं होगा।
हल सहित उदाहरण
यदि A, B और C एक रेखा पर स्थित तीन बिंदु हैं और B बिंदुओं A और B के बीच में स्थित है तो सिद्ध कीजिए कि AB + BC = AC है।
हल:
AB + BC के साथ AC संपाती है।
साथ ही, यूक्लिड का अभिगृहीत (4) कहता है कि वे वस्तुएँ जो परस्पर संपाती हों एक दूसरे के बराबर होती हैं। अतः, यह सिद्ध किया जा सकता है कि
AB + BC = AC
है। ध्यान दीजिए कि इस हल में यह मान लिया गया है कि दो बिंदुओं से होकर एक अद्वितीय रेखा खींची जा सकती है।
यूक्लिड की अभिधारणाएँ
यूक्लिड की पाँच अभिधारणायें इस प्रकार हैंः
अभिधारणा 1:
एक बिंदु से एक अन्य बिंदु तक एक सीधी रेखा खींची जा सकती है।
यह अभिधारणा हमें बताती है कि दो भिन्न बिंदुओं से होकर कम से कम एक रेखा अवश्य खींची जा सकती है।
अभिधारणा 2:
एक सांत रेखा को अनिश्चित रूप से बढ़ाया जा सकता है।
ध्यान दीजिए जिसको हम आजकल रेखाखंड कहते हैं, उसे यूक्लिड ने सांत रेखा कहा था। अतः, वर्तमान की भाषा में, दूसरी अभिधारणा यह कहती है कि एक रेखाखंड को दोनों ओर विस्तृत करके एक रेखा बनाई जा सकती है।
अभिधारणा 3:
किसी को केन्द्र मान कर और किसी त्रिज्या से एक वृत्त खींचा जा सकता है।
अभिधारणा 4:
सभी समकोण एक दूसरे के बराबर होते हैं।
अभिधारणा 5:
यदि एक सीधी रेखा दो सीधी रेखाओं पर गिर कर अपने एक ही ओर दो अंतः कोण इस प्रकार बनाए कि इन दोनों कोणों का योग मिल कर दो समकोणों से कम हो, तो वे दोनों सीधी रेखाएँ अनिश्चित रूप से बढ़ाए जाने पर उसी ओर मिलती हैं जिस ओर यह योग दो समकोणों से कम होता है।
यूक्लिड की पाँचवीं अभिधारणा के समतुल्य रूपान्तरण
गणित के इतिहास में यूक्लिड की पाँचवीं अभिधारणा का अत्याधिक महत्व है। इस अभिधारणा के परिणामस्वरूप यदि दो रेखाओं पर गिरने वाली रेखा के एक ही ओर के दोनों अंतः कोणों का योग 180⁰ हो, तो दोनों रेखाएँ कभी भी प्रतिच्छेद नहीं कर सकतीं।
यूक्लिड ज्यामिति का इतिहास
हड़प्पा और मोहनजो-दारो में खुदाई सिंधु घाटी सभ्यता (लगभग 3300-1300 ईसा पूर्व) के अत्यंत सुनियोजित शहरों को दर्शाती है। मिस्रवासियों द्वारा पिरामिडों का निर्दोष निर्माण उस समय के लोगों द्वारा उपयोग की जाने वाली ज्यामितीय तकनीकों के व्यापक उपयोग का एक और उदाहरण है। भारत में, सुलबा सूत्र, ज्यामिति पर पाठ्यपुस्तकें दर्शाती हैं कि भारतीय वैदिक काल में ज्यामिति की परंपरा थी।
ज्यामिति का विकास धीरे-धीरे हो रहा था, जब मिस्र के अलेक्जेंड्रिया में गणित के शिक्षक यूक्लिड ने ज्यामिति में इनमें से अधिकांश विकासों को एकत्र किया और इसे अपने प्रसिद्ध ग्रंथ में संकलित किया, जिसे उन्होंने ‘एलिमेंट्स’ नाम दिया।
| समतल ज्यामिति | ठोस ज्यामिति |
|
|
यूक्लिडियन ज्यामिति के उदाहरण
- यूक्लिडियन ज्यामिति के दो सामान्य उदाहरण कोण और वृत्त हैं। कोणों को दो सीधी रेखाओं का झुकाव कहा जाता है। एक वृत्त एक समतल आकृति है, जिसमें केंद्र से एक स्थिर दूरी (त्रिज्या कहा जाता है) पर सभी बिंदु होते हैं।
यूक्लिडियन और गैर-यूक्लिडियन ज्यामिति
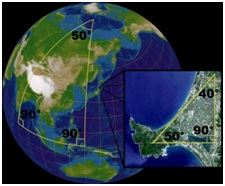
- समानांतर रेखाओं की प्रकृति में यूक्लिडियन और गैर-यूक्लिडियन ज्यामिति में अंतर होता है। यूक्लिडियन ज्यामिति में, दिए गए बिंदु और रेखा के लिए, बिल्कुल एक ही रेखा होती है जो एक ही तल में दिए गए बिंदुओं से होकर गुजरती है और यह कभी भी प्रतिच्छेद नहीं करती है।यह गैर-यूक्लिडियन यूक्लिडियन ज्यामिति से अलग है। गोलाकार ज्यामिति गैर-यूक्लिडियन ज्यामिति का एक उदाहरण है क्योंकि यहां रेखाएं सीधी नहीं हैं।
दैनिक जीवन में ज्यामिति
- ज्यामिति एक प्राचीन विज्ञान और गणित की एक महत्वपूर्ण शाखा है। प्राचीन गणितज्ञ यूक्लिड को ज्यामिति के पिता के रूप में श्रेय दिया जाता है, जिन्होंने औपचारिक रूप से अपनी पुस्तक “एलिमेंट्स” में इस शब्द का इस्तेमाल किया। यह पुराने ग्रीक शब्द जियोमेट्रॉन से लिया गया है जिसका अर्थ है पृथ्वी को मापना (भू: पृथ्वी और मेट्रोन: माप)। एक प्राथमिक या मध्य विद्यालय के छात्र के लिए, यह उनके नामकरण, गुण और उनके क्षेत्रों और मात्राओं से संबंधित सूत्रों सहित विभिन्न बुनियादी आकृतियों के बारे में है। लेकिन आधुनिक ज्यामिति इन बुनियादी अवधारणाओं से बहुत अधिक अलग हो गई है। लेकिन इनमें से किसी ने भी अपने अस्तित्व और दैनिक जीवन में अनुप्रयोगों को नहीं बदला है, और यह अभी भी हमारे दैनिक अनुभव में परिलक्षित होता है
- ।ज्यामिति गणित की सबसे प्रभावशाली शाखा है। एक गहन अवलोकन आपको कई उदाहरण देगा। इसे प्राचीन युग में ढाला गया था; इसलिए जीवन पर इसका प्रभाव भी व्यापक है। यह एक संभावित समस्या समाधान है, खासकर व्यावहारिक जीवन में। इसके अनुप्रयोग बहुत पहले मिस्र की सभ्यता के दौरान शुरू हुए थे। उन्होंने कला, माप और वास्तुकला जैसे विभिन्न क्षेत्रों में ज्यामिति का उपयोग किया। भव्य मंदिर, महल, बांध और पुल इन्हीं के परिणाम हैं। निर्माण और माप के अलावा, इसने इंजीनियरिंग, जैव रासायनिक मॉडलिंग, डिजाइनिंग, कंप्यूटर ग्राफिक्स और टाइपोग्राफी के कई और क्षेत्रों को प्रभावित किया है।
- रोजाना हम ज्योमेट्री की मदद से बहुत सारे काम करते हैं। कुछ सामान्य अनुप्रयोगों में भूमि की एक रेखा और सतह क्षेत्र का मापन, उपहार लपेटना, अतिप्रवाह के बिना एक बॉक्स या टिफिन भरना, विभिन्न साइनबोर्ड के लिए उपयोग किए जाने वाले आकार शामिल हैं। ज्यामिति का अच्छा व्यावहारिक ज्ञान रखने वाला व्यक्ति संघर्ष की संभावना के बिना भूमि के आयामों को मापने में स्वयं की सहायता कर सकता है। अन्य उन्नत अनुप्रयोगों में रोबोटिक्स, फैशन डिजाइनिंग, कंप्यूटर ग्राफिक्स और मॉडलिंग शामिल हैं। उदाहरण के लिए, फैशन डिजाइनिंग में, एक फैशन डिजाइनर को सर्वोत्तम डिजाइन विकसित करने के लिए विभिन्न आकृतियों और उनकी समरूपता के बारे में जानना होता है।
विश्लेषणात्मक ज्यामिति
- विश्लेषणात्मक ज्यामिति बीजगणित की एक शाखा है, जो डेसकार्टेस और फ़र्मेट का एक महान आविष्कार है, जो कुछ ज्यामितीय वस्तुओं, जैसे कि रेखाएं, बिंदु, वक्र, और इसी तरह के मॉडलिंग से संबंधित है। यह एक गणितीय विषय है जो समस्याओं को हल करने के लिए बीजीय प्रतीकवाद और विधियों का उपयोग करता है। यह बीजीय समीकरणों और ज्यामितीय वक्रों के बीच सामंजस्य स्थापित करता है। विश्लेषणात्मक ज्यामिति का प्रतिनिधित्व करने के लिए उपयोग किया जाने वाला वैकल्पिक शब्द “कोऑर्डिनेट ज्योमेट्री” है।
- इसमें कुछ महत्वपूर्ण विषय शामिल हैं जैसे मध्यबिंदु और दूरी, समन्वय तल पर समानांतर और लंबवत रेखाएं, विभाजन रेखा खंड, रेखा और बिंदु के बीच की दूरी। विश्लेषणात्मक ज्यामिति का अध्ययन महत्वपूर्ण है क्योंकि यह गणित के अगले स्तर के लिए ज्ञान देता है। यह तार्किक सोच और समस्या समाधान कौशल सीखने का पारंपरिक तरीका है। आइए विश्लेषणात्मक ज्यामिति, सूत्रों, कार्टेशियन समतल, विश्लेषणात्मक ज्यामिति में तीन आयामों, इसके अनुप्रयोगों और कुछ हल की गई समस्याओं में प्रयुक्त शब्दों पर चर्चा करें।
समतल
यह समझने के लिए कि विश्लेषणात्मक ज्यामिति कैसे महत्वपूर्ण और उपयोगी है, सबसे पहले, हमें यह सीखना होगा कि एक समतल क्या है? यदि एक समान सीधी सतह दोनों दिशाओं में अपरिमित रूप से चलती है, तो इसे समतल कहते हैं। इसलिए, यदि आप इस तल पर कोई बिंदु पाते हैं, तो विश्लेषणात्मक ज्यामिति का उपयोग करके इसका पता लगाना आसान है। आपको बस X और Y तल में बिंदु के निर्देशांक जानने की आवश्यकता है।
निर्देशांक
निर्देशांक दो क्रमित युग्म हैं, जो एक समतल में किसी दिए गए बिंदु के स्थान को परिभाषित करते हैं। आइए इसे नीचे दिए गए बॉक्स की मदद से समझते हैं।

उपरोक्त ग्रिड में, कॉलम को ए, बी, सी के रूप में दर्शाया गया है, और पंक्तियों को 1, 2, 3 के रूप में दर्शाया गया है।
अक्षर x की स्थिति B2 यानी कॉलम B और पंक्ति 2 है। तो, B और 2 इस बॉक्स x के निर्देशांक हैं।
चूंकि प्रत्येक कॉलम और पंक्तियों में कई बॉक्स होते हैं, लेकिन केवल एक बॉक्स में बिंदु x होता है, और हम उस बॉक्स की पंक्ति और कॉलम के प्रतिच्छेदन का पता लगाकर उसका स्थान ढूंढ सकते हैं। विश्लेषणात्मक ज्यामिति में विभिन्न प्रकार के निर्देशांक होते हैं। उनमें से कुछ इस प्रकार हैं:
- कार्तीय निर्देशांक
- धुवीय निर्देशांक
- बेलनाकार निर्देशांक
- गोलाकार निर्देशांक
आइए इन सभी प्रकार के निर्देशांकों की चर्चा यहां संक्षेप में करें।
कार्तीय निर्देशांक
सबसे प्रसिद्ध समन्वय प्रणाली कार्तीय निर्देशांक का उपयोग करने के लिए है, जहां प्रत्येक बिंदु में एक x-निर्देशांक और y-निर्देशांक होता है जो क्रमशः अपनी क्षैतिज स्थिति और ऊर्ध्वाधर स्थिति को व्यक्त करता है। उन्हें आमतौर पर एक आदेशित जोड़ी के रूप में संबोधित किया जाता है और (x, y) के रूप में दर्शाया जाता है। हम इस प्रणाली का उपयोग त्रि-आयामी ज्यामिति के लिए भी कर सकते हैं, जहां प्रत्येक बिंदु को यूक्लिडियन अंतरिक्ष में निर्देशांक (x, y, z) के एक क्रमबद्ध निर्देशांक द्वारा दर्शाया जाता है।
धुवीय निर्देशांक
ध्रुवीय निर्देशांकों के मामले में, समतल में प्रत्येक बिंदु को मूल बिन्दु से ‘r’ की दूरी और ध्रुवीय अक्ष से ![]() कोण द्वारा दर्शाया जाता है।
कोण द्वारा दर्शाया जाता है।
बेलनाकार निर्देशांक
बेलनाकार निर्देशांक के मामले में, सभी बिंदुओं को उनकी ऊंचाई, z-अक्ष से त्रिज्या और क्षैतिज अक्ष के संबंध में xy-तल पर प्रक्षेपित कोण द्वारा दर्शाया जाता है। ऊंचाई, त्रिज्या और कोण को क्रमशः h, r और द्वारा दर्शाया जाता है।
गोलाकार निर्देशांक
गोलाकार निर्देशांक में, अंतरिक्ष में बिंदु को मूल (ρ) से इसकी दूरी, क्षैतिज अक्ष (θ) के संबंध में xy-तल पर प्रक्षेपित कोण और z- अक्ष के संबंध में एक अन्य कोण (φ) द्वारा दर्शाया जाता है।
कार्टेशियन समतल
निर्देशांक ज्यामिति में, प्रत्येक बिंदु को निर्देशांक तल या कार्तीय तल पर ही स्थित कहा जाता है।
नीचे दिए गए चित्र को देखें।
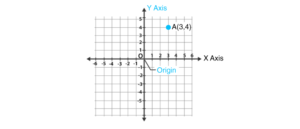
उपरोक्त ग्राफ में स्केल के रूप में x-अक्ष और y-अक्ष है। x-अक्ष समतल पर चल रहा है और Y-अक्ष x-अक्ष के समकोण पर चल रहा है। यह ऊपर बताए गए बॉक्स के समान है।
आइए निर्देशांक के बारे में अधिक जानें:
उत्पत्ति: यह अक्ष (x-अक्ष और y-अक्ष) का प्रतिच्छेदन बिंदु है। इस बिंदु पर x और y-अक्ष दोनों शून्य हैं।
अक्ष के विभिन्न पक्षों के मान
- x-अक्ष – इस अक्ष के दायीं ओर के मान धनात्मक होते हैं और बाईं ओर के मान ऋणात्मक होते हैं।
- y-अक्ष – मूल के ऊपर का मान धनात्मक होता है और मूल के नीचे का मान ऋणात्मक होता है।
- एक बिंदु का पता लगाने के लिए: हमें पहले x-अक्ष और y-अक्ष के स्थान को लिखने के क्रम में समतल का पता लगाने के लिए दो संख्याओं की आवश्यकता होती है। दोनों समतल में सिंगल और यूनिक पोजीशन बताएंगे। आपको तल पर बिंदुओं के क्रम का अनिवार्य रूप से पालन करने की आवश्यकता है, अर्थात x निर्देशांक हमेशा युग्म में पहला होता है। (x,y)।
- यदि आप ऊपर दिए गए चित्र को देखें, तो बिंदु A का x-अक्ष पर मान 3 और Y-अक्ष पर मान 2 है। ये बिंदु A के आयताकार र्देशांक हैं जिन्हें (3, 2) के रूप में दर्शाया गया है।
- कार्टेशियन निर्देशांक का उपयोग करके, हम एक सीधी रेखा के समीकरण, समतल के समीकरण, वर्गों और अक्सर त्रि-आयामी ज्यामिति में परिभाषित कर सकते हैं। विश्लेषणात्मक ज्यामिति का मुख्य कार्य यह है कि यह संख्यात्मक तरीके से विभिन्न ज्यामितीय आकृतियों को परिभाषित और प्रस्तुत करता है। यह आकृतियों से संख्यात्मक जानकारी भी निकालता है।
विश्लेषणात्मक ज्यामिति सूत्र
ग्राफ़ और निर्देशांक का उपयोग ज्यामितीय आकृतियों के मापन के लिए किया जाता है। विश्लेषणात्मक ज्यामिति में कई महत्वपूर्ण सूत्र हैं। चूंकि विज्ञान और इंजीनियरिंग में अलग-अलग मात्राओं में परिवर्तन की दर का अध्ययन शामिल है, यह शामिल मात्राओं के बीच संबंध दिखाने में मदद करता है। गणित की शाखा जिसे “कैलकुलस” कहा जाता है, को विश्लेषणात्मक ज्यामिति की स्पष्ट समझ की आवश्यकता होती है। यहाँ, कुछ महत्वपूर्ण सूत्रो का उपयोग दूरी, ढलान खोजने या रेखा के समीकरण को खोजने के लिए किया जा रहा है।
दूरी सूत्र
मान लीजिए कि दो बिंदु A और B हैं, जिनके निर्देशांक क्रमशः (x1, y1) और (x2, y2) हैं।
इस प्रकार, दो बिंदुओं के बीच की दूरी इस प्रकार दी गई है-
![]()
मध्यबिंदु प्रमेय सूत्र
मान लीजिए कि A और B एक समतल में कुछ बिंदु हैं, जो क्रमशः निर्देशांक (x1, y1) और (x2, y2) वाली एक रेखा बनाने के लिए जुड़े हुए हैं। मान लीजिए, M (x, y) बिंदु A और B को जोड़ने वाली रेखा का मध्यबिंदु है तो इसका सूत्र दिया जाता है;
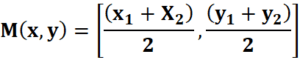
कोण सूत्र
मान लीजिए कि दो रेखाओं का ढलान m1 और m2 है और θ दो रेखाओं A और B के बीच बना कोण है, जिसे इस प्रकार दर्शाया गया है:
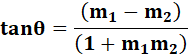
धारा सूत्र
मान लीजिए कि दो रेखाएँ A और B में क्रमशः निर्देशांक (x1, y1) और (x2, y2) हैं। एक बिंदु P दो रेखाएँ m:n के अनुपात में है, तो P के निर्देशांक हैं:
जब अनुपात m:n आंतरिक है
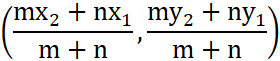
जब अनुपात m:n बाहरी है
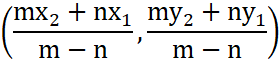
We hope that class 9 Math Chapter 5 यूक्लिड की ज्यामिति का परिचय (Introduction to Euclid’s Geometry) Notes in Hindi helped you. If you have any queries about class 9 Math Chapter 5 यूक्लिड की ज्यामिति का परिचय (Introduction to Euclid’s Geometry) Notes in Hindi or about any other Notes of class 9 Math in Hindi, so you can comment below. We will reach you as soon as possible…