पाठ – 1
संख्या पद्धति
In this post we have given the detailed notes of class 9 Math chapter 1 Number Systems in Hindi. These notes are useful for the students who are going to appear in class 9 board exams.
इस पोस्ट में कक्षा 9 के गणित के पाठ 1 संख्या पद्धति के नोट्स दिये गए है। यह उन सभी विद्यार्थियों के लिए आवश्यक है जो इस वर्ष कक्षा 9 में है एवं गणित विषय पढ़ रहे है।
| Board | CBSE Board, UP Board, JAC Board, Bihar Board, HBSE Board, UBSE Board, PSEB Board, RBSE Board, CGBSE Board, MPBSE Board |
| Textbook | NCERT |
| Class | Class 9 |
| Subject | Math |
| Chapter no. | Chapter 1 |
| Chapter Name | संख्या पद्धति (Number Systems) |
| Category | Class 9 Math Notes in Hindi |
| Medium | Hindi |
पाठ 1, संख्या पद्धति
संख्या पद्धतियाँ
संख्याओं को लिखने एवं उनके नामकरण के सुव्यवस्थित नियमों को संख्या पद्धति कहते हैं। इसके लिये निर्धारित प्रतीकों का प्रयोग किया जाता है जिनकी संख्या निश्चित एवं सीमित होती है।
संख्याओं के प्रकार
संख्याएं निम्नलिखित प्रकार की होती हैं:
- प्राकृतिक संख्या
- सम संख्या
- विषम संख्या
- पूर्ण संख्या
- पूर्णांक संख्या
- भाज्य संख्या
- अभाज्य संख्या
- सह अभाज्य संख्या
- परिमेय संख्या
- अपरिमेय संख्या
- वास्तविक संख्या
- अवास्तविक संख्या
1. प्राकृतिक संख्या
गणित में 1,2,3,… इत्यादि संख्याओं को प्राकृतिक संख्याएँ (अंग्रेज़ी: natural numbers) कहते हैं। ये संख्याएँ वस्तुओं को गिनने (“मेज पर 5 किताबें हैं”) अथवा क्रम में रखने (“मैंने स्पर्धा में 6वाँ स्थान पाया”) के लिए प्रयुक्त होती हैं।
प्राकृतिक संख्याओं के जो गुणस्वभाव भाज्यता से संबंधित हैं।
उदाहरण: (ऊपर से नीचे की ओर) एक सेब, दो सेब, तीन सेब, ..

2. सम संख्या
कोई भी संख्या जो 2 से विभक्त होती है सम संख्या कहलाती है। जैसे 0, 2,4,6,-2 आदि। इसलिए 2 एक सम संख्या है।
उदाहरण: संख्या दो से भाग देकर
सम संख्याओं पहचानने का दूसरा तरीका है कि आप दी हुई संख्या को 2 से भाग दे। और यदि शेषफल शून्य आता है या पूरी तरह से विभाजित हो जाता है तो वो सम संख्या है। और इस तरीका को भी आसान ही कहेंगे क्योंकि 5-6 अंको की संख्या को 2 से भाग देना कोई भारी काम नहीं है।
जैसे-
6668 – शेषफल 0 प्राप्त होता है इसलिए यह एक सम संख्या है।
2245 – शेषफल 1 प्राप्त होता है इसलिए यह सम संख्या नहीं है।
3. विषम संख्या
ऐसी प्राकृतिक संख्या जो 2 से पूर्णतः से विभाजित न हो उन्हें विषम संख्याएँ कहते हैं।
जैसे :- 1, 3, 5, 7, 9, 11, ………
जिस संख्या के अंत में 1, 3, 5, 7, 9 आता हैं वो सभी विषम संख्याएँ कहलाती हैं।
विषम संख्या को अंग्रेजी में Odd Number कहते हैं।
4. पूर्ण संख्या
0 से अनंत तक की सभी धनात्मक प्राकृत संख्याओं को पूर्ण संख्या कहते है। अर्थात सभी धनात्मक प्राकृत संख्याएँ (Natural Numbers) पूर्ण संख्या होती है।
उदाहरण :- 0,1,2,3,4,5,6,7…………. अनंत
संख्या रेखा पर पूर्ण संख्या
0 और 1 से नामांकित इन बिंदुओं के बीच की दूरी एक मात्रक दूरी (unit distance) कहलाती है। इसी रेखा पर 1 के दाईं ओर 1 मात्रक दूरी पर एक बिंदु अंकित कीजिए और 2 से नामांकित कीजिए। इसी विधि का प्रयोग करते हुए, संख्या रेखा पर एक-एक मात्रक दूरी पर बिंदुओं को 3, 4, 5, … से नामांकित करते रहिए। अब आप जब दाईं ओर आगे बढ़ेंगे तो आप किसी भी पूर्ण संख्या प्राप्त कर सकते हैं।
![]()
संख्या रेखा
5. पूर्णांक संख्या
सभी पूर्ण संख्याओं और ऋणात्मक संख्याओं के एक सम्मिलित समूह (संग्रह) को , पूर्णांक कहते है। अर्थात पूर्ण संख्या के साथ यदि ऋणात्मक संख्याओं को सम्मिलित कर लिया जाये तो प्राप्त समूह को पूर्णांक संख्या कहते है।
Examples:- 4,5,0,-2,-1,55,-60 सभी पूर्णांक संख्याए है।
6. भाज्य संख्या
ऐसी प्राकृत संख्या जो स्वंय और 1 से विभाजित होने के अतिरिक्त कम से कम किसी एक अन्य संख्या से विभाजित हो उन्हें भाज्य संख्या कहते हैं।
Ex : 4, 6, 8, 9, 10, 12, ………∞
भाज्य संख्या को अंग्रेजी में “Composite Number” कहाँ जाता हैं।
भाज्य संख्याएँ कैसे निकालें
जिस संख्या का गुणनखण्ड दो या दो से अधिक हो वे सभी धनात्मक पूर्णाक संख्याएँ भाज्य संख्या कहलाती हैं।
आसान भाषा में समझा जाए तो – तीन या तीन से अधिक गुणनखण्ड वाले धनात्मक संख्या को भाज्य संख्या कहते हैं।
जैसे:-
- 18 ÷ 1 = 18
- 18 ÷ 2 = 9
- 18 ÷ 3 = 6
- 18 ÷ 9 = 2
- 18 ÷ 18 = 1
7. अभाज्य संख्या
अभाज्य संख्याएँ: वे संख्याएँ जो स्वयं और 1 के अतिरिक्त अन्य किसी भी संख्या से विभाजित नहीं हो उन्हें ‘अभाज्य संख्याएँ’ कहते हैं।
जैसे- 2, 3, 7, 11, 13, 17 ………. आदि ‘अभाज्य संख्याएँ’ हैं। ‘1’ एक विशेष संख्या है जो न तो अभाज्य संख्या है और न ही भाज्य संख्या है।
8. सह अभाज्य संख्या
ऐसी संख्याओं के जोड़े जिनके गुणनखण्डों में 1 के अतिरिक्त कोई भी उभयनिष्ठ गुणनखण्ड न हो उन्हें सह अभाज्य संख्या कहते हैं।
दूसरे शब्दों में – कम से कम 2 अभाज्य संख्याओ का ऐसा समूह जिसका (HCF) 1 हो सह अभाज्य संख्याएँ कहलाती हैं।
HCF का मतलब सबसे बड़ा सार्व गुणनखण्ड होता हैं। जैसे :- 9, 25 में सबसे बड़ा सार्व गुणनखण्ड केवल 1 ही हैं। अतः (9, 25) एक सह अभाज्य संख्या हैं।
उदाहरण :- (2, 3), (3, 4), (5, 6), (14, 15),…………….दी गई संख्याओं में से कौनसा गुणनखण्ड सह-अभाज्य संख्याएँ हैं?
हल:- (2, 3), (3, 4), (5, 6), (14, 15),
सह अभाज्य संख्याओं को हम इस प्रकार भी समझ सकते हैं –
जैसे:-
- (2, 3)
- 2 × 1 = 2
- 3 × 1 = 3
- (3, 4)
- 3 × 1 = 3
- 4 × 1 = 4
- (5, 6)
- 5 × 1 = 5
- 6 × 1 = 6
- (14, 15)
- 14 × 1 = 14
- 15 × 1 = 15
गुणनखण्ड में आप देख सकते हैं कि सभी में उभयनिष्ठ 1 प्राप्त होता हैं अर्थात यह सह अभाज्य संख्याएँ हैं।
9. परिमेय संख्या
वैसी वास्तविक संख्याएँ जो p/q के लघुतम स्वरुप में व्यवस्थित हो, जहा p और q पूर्णांक होने के साथ साथ q शून्य के बराबर न हो, उसे परिमेय संख्या कहा जाता है।
अर्थात, हर और अंश के रूप में लिखी जाने वाली सभी संख्याएँ परिमेय संख्या कहलाती है. जहाँ केवल हर शून्य के बराबर न हो। स्पष्ट शब्दों में, एक पूर्णांक संख्या को दूसरे पूर्णांक से भाग देने के उपरांत जो संख्या प्राप्त होती है, उसे परिमेय संख्या कहते है।
दुसरें शब्दों में, वैसी संख्या जो p/q के रूप में लिखी जा सके, जहाँ p और q पूर्णांक हो तथा q ≠ 0 हो, उसे परिमेय संख्या कहते है।
जैसे; ![]() ,
, ![]() ,
, ![]()
आदि।
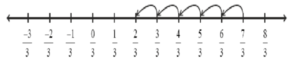
उदाहरण 1 और 2 के बीच की पाँच परिमेय संख्याएँ ज्ञात कीजिए।
हल: r और s के बीच की एक परिमेय संख्या ज्ञात करने के लिए r और s को जोड़ते हैं और उसे दो से भाग दे देते हैं,
अर्थात् ![]() r और s के बीच स्थित होती है। अतः
r और s के बीच स्थित होती है। अतः ![]() 1 और 2 के बीच की एक संख्या है। इसी प्रक्रिया में हम 1 और 2 के बीच चार और परिमेय संख्याएँ ज्ञात कर सकते हैं। ये चार संख्याएँ हैं:
1 और 2 के बीच की एक संख्या है। इसी प्रक्रिया में हम 1 और 2 के बीच चार और परिमेय संख्याएँ ज्ञात कर सकते हैं। ये चार संख्याएँ हैं: ![]() और।
और।
परिमेय संख्या के गुणधर्म | Property of Rational Numbers in Hindi
चूंकि Parimey Sankhya वास्तविक संख्या का एक भाग है, इसलिए परिमेय संख्या वास्तविक संख्या प्रणाली के सभी गुणों का पालन करता है। इसके अलावा भी कुछ गुण है जो निचे अंकित है।
- परिमेय संख्याओं को संख्या रेखा पर पूर्णांक की तरह ही निरूपित किया जा सकता है।
- यदि दो परिमेय संख्याओं को जोड़, घटाव, गुना या भाग किया जाए, तो हमेशा परिमेय संख्या ही प्राप्त होता है।
- परिमेय संख्या के अंश और हर में बराबर संख्या से गुना या भाग किया जाए, तो परिमेय संख्या ही प्राप्त होगा।
- परिमेय संख्याओं का योगफल और गुणनफल की संक्रियाएँ क्रमविनिमेय साहचर्य होती है।
10. अपरिमेय संख्या
ऐसी संख्याएँ जिन्हें p/q के रूप में नहीं लिखा जा सकता अपरिमेय संख्याएँ कहलाती हैं।
जैसे- π, φ, √5, √7, √13 आदि।
धनात्मक परिमेय और ऋणात्मक परिमेय संख्याओं में अंतर
परिमेय संख्या p/q के रूप में होती है, जहाँ p/q दोनों पूर्णांक होते है। (q या हर) हमेशा शून्य के बराबर नहीं होता है। वहाँ परिमेय संख्याएँ धनात्मक और ऋणात्मक हो सकती हैं।
संख्याएँ धनात्मक परिमेय होगी यदि और केवल यदि (+p/+q) हो ऋणात्मक परिमेय संख्याएँ होगीं यदि और केवल यदि -(p/q) हो।
धनात्मक परिमेय संख्याएँ | ऋणात्मक परिमेय संख्याएँ |
परिमेय संख्या जिनमें अंश तथा हर दोनों धनात्मक हों, धनात्मक परिमेय संख्याएँ कहलाती हैं। | परिमेय संख्या जिनमें अंश या हर कोई एक ऋणात्मक हो ऋणात्मक परिमेय संख्याएँ कहते हैं। |
अंश और हर दोनों में बराबर चिन्ह हो। अर्थात (p/q) या (+p/+q) हो वह धनात्मक परिमेय संख्याएँ होगी। | यदि अंश और हर दोनों एक दूसरे के विपरीत चिन्ह के हो, अर्थात -(p/q) = (-p)/q = p/(-q), हो तो वह ऋणात्मक परिमेय संख्याएँ कहलाती हैं। |
धनात्मक परिमेय संख्याएँ शून्य से बड़ी होती हैं। | ऋणात्मक परिमेय संख्याएँ शून्य से छोटी होती हैं। |
धनात्मक परिमेय संख्याएँ के उदाहरण :- | धनात्मक परिमेय संख्याएँ के उदाहरण :- |
समतुल्य परिमेय संख्याएँ
ऐसी परिमेय संख्याएँ जो परस्पर एक-दूसरे के बराबर हों उन संख्याओं को एक दूसरे के समतुल्य परिमेय संख्याएँ कहाँ जाता है।
दी हुई परिमेय संख्याएँ के समतुल्य परिमेय संख्याएँ निकालना
एक परिमेय संख्या के अंश और हर को एक ही शून्येतर पूर्णांक से गुणा करने पर दी हुई परिमेय संख्या के समतुल्य या तुल्य एक अन्य परिमेय संख्या प्राप्त होती है।
उदाहरण
![]() के अंश और हर में 2 से गुणा करने पर प्राप्त संख्या
के अंश और हर में 2 से गुणा करने पर प्राप्त संख्या ![]() के समतुल्य परिमेय संख्याएँ होगी।
के समतुल्य परिमेय संख्याएँ होगी।
![]() =
= ![]()
![]() =
= ![]()
अतः ![]() समतुल्य
समतुल्य ![]() परिमेय संख्याएँ हैं।
परिमेय संख्याएँ हैं।
उसी प्रकार ![]() =
= ![]()
![]() =
= ![]()
अतः ![]() समतुल्य
समतुल्य ![]() परिमेय संख्याएँ हैं।
परिमेय संख्याएँ हैं।
उसी प्रकार ![]() =
= ![]()
![]() =
= ![]()
अतः ![]() समतुल्य
समतुल्य ![]() परिमेय संख्याएँ हैं।
परिमेय संख्याएँ हैं।
अतः ![]() ,
, ![]() ,
, ![]() और
और ![]() समतुल्य परिमेय संख्याएँ हैं क्योंकि ये आपस में परस्पर बराबर हैं।
समतुल्य परिमेय संख्याएँ हैं क्योंकि ये आपस में परस्पर बराबर हैं।
परिमेय संख्याओं से संबंधित उदाहरण
उदाहरण (1) ![]()
तथा ![]() की तुलना कीजिए?
की तुलना कीजिए?
हल:- प्रश्नानानुसार,
![]() तथा
तथा ![]()
इन दोनों परिमेय संख्याओं के हर 2 तथा 3 का लघुत्तम समापवर्तक होता है 3 × 2 = 6
अत: ![]() =
= ![]() =
= ![]()
तथा, ![]() =
= ![]() =
= ![]()
अब चूँकि ![]() तथा
तथा ![]() के अंश में 6 बड़ा है अत:
के अंश में 6 बड़ा है अत:
 >
> 
या,  >
> 
अर्थात ![]() बड़ा है
बड़ा है ![]() से।
से।
उत्तर:-  >
> 
उदाहरण (2) परिमेय संख्याएँ ![]() तथा
तथा ![]() की तुलना कीजिए?
की तुलना कीजिए?
हल:- प्रश्नानानुसार,
दी गयी परिमेय संख्याएँ ![]() तथा
तथा ![]()
बज्र गुणन करने पर
बज्र गुणन
3 × 7 तथा 6 × 5
21 तथा 30
21 < 30
अत: ![]() <
< ![]()
अर्थात, ![]() छोटा है
छोटा है ![]() से
से
उत्तर:-  <
< 
11. वास्तविक संख्या
परिमेय और अपरिमेय संख्याओं के समूह को वास्तविक संख्या कहते है। तथा वास्तविक संख्याओं को R से सूचित किया जाता है। पूर्ण, प्राकृत, पूर्णांक, परिमेय तथा अपरिमेय संख्याओं के समूह को वास्तविक संख्या (Real number) कहते है।
जैसे- 2 , ![]() , 9 ,
, 9 , ![]() ,
, ![]() , -5, pi (
, -5, pi ( ![]() ), -100 आदि सभी वास्तविक संख्याएँ है।
), -100 आदि सभी वास्तविक संख्याएँ है।
12. अवास्तविक संख्या
अवास्तविक संख्या यदि किसी संख्या का वर्ग ऋणात्मक संख्या हो ,तो वैसी संख्याये अवास्तविक कहलाती है । अवास्तविक संख्याये ![]() ,√-4 ,
,√-4 , ![]()
के रूप में लिखी जाती है । जो संख्याये वास्तविक तथा अवास्तविक संख्याओं से मिलकर बनती है ,जैसे 3+√-4, समिश्र संख्याये कहलाती है ।
जैसे:- ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]()
अवास्तविक संख्याओं को √-3 , √-5 , ![]() ,
, ![]() ,
, ![]() के रूप में लिखा जाता है।
के रूप में लिखा जाता है।
मुख्य अवधारणाएँ और परिणाम
- परिमेय संख्याएँ
- अपरिमेय संख्याएँ
- संख्या रेखा पर अपरिमेय संख्याएँ निर्धारित करना
- वास्तविक संख्याएँ और उनके दशमलव प्रसार
- संख्या रेखा पर वास्तविक संख्याओं का निरूपण
- वास्तविक संख्याओं पर संक्रियाएँ
- हर का परिमेयीकरण
वास्तविक संख्याओं के लिए घातांकों के नियम
- एक संख्या परिमेय संख्या कहलाती है, यदि उसे p/q के रूप में लिखा जा सके, जहाँ p और q पूर्णांक हैं तथा q ≠ 0 है।
- एक संख्या जिसे p/q के रूप में न लिखा जा सके (जहाँ p और q पूर्णांक हैं तथा q ≠ 0 है) अपरिमेय संख्या कहलाती है।
- सभी परिमेय संख्याओं और अपरिमेय संख्याओं को मिलाकर वास्तविक संख्याओं का संग्रह कहा जाता है।
- एक परिमेय संख्या का दशमलव प्रसार सांत या असांत आवर्ती होता है तथा एक अपरिमेय संख्या का दशमलव प्रसार असांत अनावर्ती होता है।
- यदि r एक परिमेय संख्या है और s एक अपरिमेय संख्या है तो r + s और r – s अपरिमेय संख्याएँ होती हैं। साथ ही, यदि r एक शून्यत्तर परिमये सख्ंया हो तो rs और r/s अपरिमेय संख्याएँ होती हैं।
धनात्मक वास्तविक संख्याओं a और b के लिए नियम
- √ab = √a √b
- √(a/b) = √a /√b
- (√a + √b) (√a – √b) = a – b
- (a + √b) (a – √b) = a² – b
- (√a + √b)² = a + 2 √ab + b
(vi) यदि m और n परिमेय संख्याएँ तथा a एक धनात्मक वास्तविक संख्या है, तो
- aᵐ aⁿ = aᵐ⁺ⁿ
- (aᵐ)ⁿ = aᵐⁿ
- aᵐ/ aⁿ = aᵐ ⁻ ⁿ
- aᵐ bᵐ = (ab)ᵐ
We hope that class 9 Math Chapter 1 संख्या पद्धति (Number Systems) Notes in Hindi helped you. If you have any queries about class 9 Math Chapter 1 संख्या पद्धति (Number Systems) Notes in Hindi or about any other Notes of class 9 Math in Hindi, so you can comment below. We will reach you as soon as possible…